I have sets of 16 note scales derived from the 31-limit tonality diamond. The Otonality is the overtones, the Utonality are the undertones. Otonal scales have the ratios of 8:9:10:11:12:13:14:15:17:19:21:23:25:27:29:31. The Utonal scales are the opposite: 32 over 16:17:18:19:20:21:22:23:24:25:26:27:28:29:31.
That gets me a matrix that is 16 by 16, or 256 notes. Click the following image to enlarge it.
Elimintating duplicates, there are 216 unique pitches per octave. Right out of the gate I have 16 major 16-note scales based on the otonality, and 16 minor scales based on the utonality. Otonality is read up and to the right, Utonality is read down and to the right, except the scale starts at the note a 3:2 below the starting point. For example, Utonality of F is on the row starting at C 1:1, and the root of the scale is F 4:3.
When I was working with the 15-limit diamond, I noticed that there were other scales, in addition to major and minor, that could be found in the diamond. In 15-limit diamond, there are two additional scales with very good 5th’s. I called one the sub-minor with a 7:6 3rd, and the other a super-major with a 9:7 3rd.
When I took a systematic look at the otonality and utonality scales in the 31-limit diamond I found other modes that could be used to construct scales with perfect major 5ths. By other modes, I mean out of each 16 note scale, start at different points in each to find interesting scales. Limiting the search to only those with perfect 5ths, I found 22 distinct modes, and with the 16 otonal and 16 utonal scales, that left a total of 191 unique and interesting scales.
The 3rds are anywhere from 7:5 subminor to 31:24 sensi supermajor.
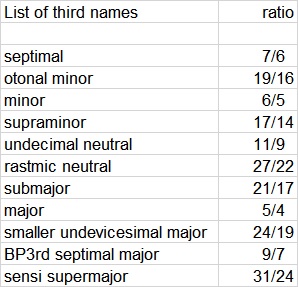
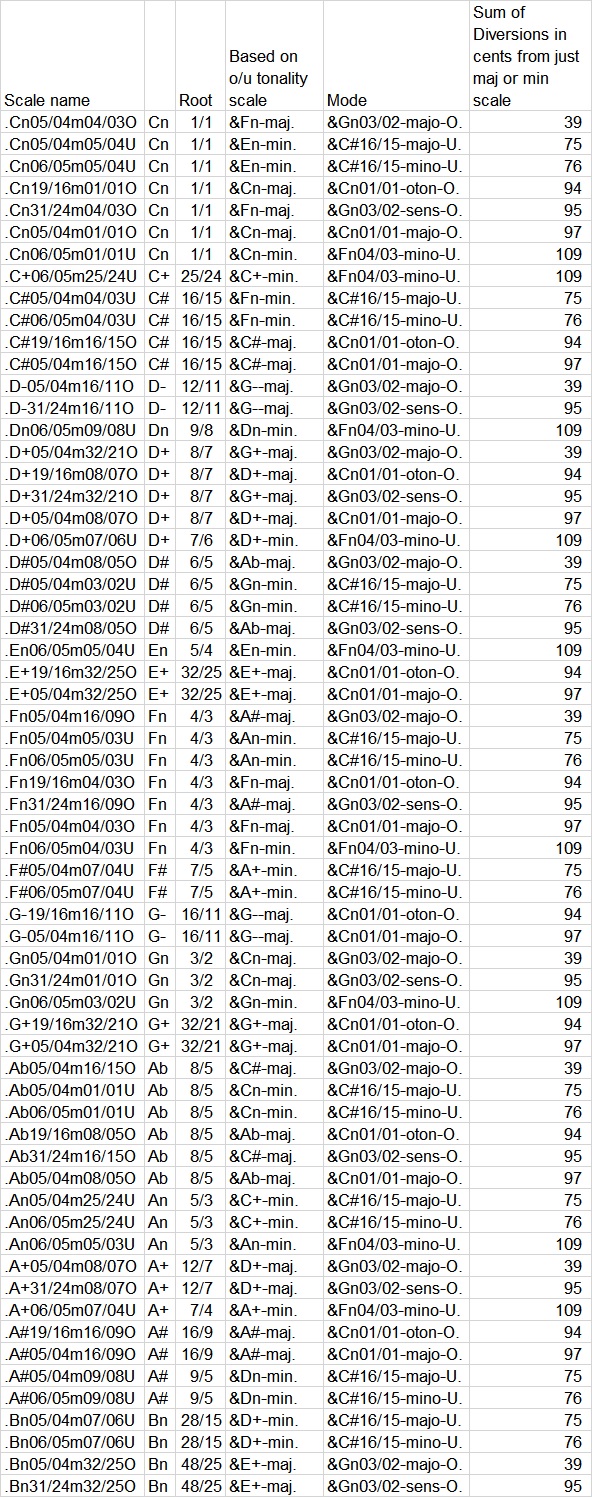
I then checked the other notes out for closeness to major or minor just. I evaluated the 2nds, 4th’s, 6th’s, and two different 7ths to see how many cents off each was, and then sorted them by distance from just. I ended up with 40 that were pretty good. In the chart below, the first column is the scale name. The first letter of the scale name is the root, the second two numbers are the third ratio, and the last two numbers are the root of the otonal (O) or utonal (U) from which the scale was derived.
For example, the first in the list starts on C, and has a 5:4 major third, and is derived from the otonal scale in the key of F. In the tonality diamond, the F otonality starts in the 9th position along the axis starting at C 1:1, then B 32:17, then A 16:9, then A 32:19, A 8:5, G 21:21, G 16:11, F 32:23, F 4:3. So the F 4:3 otonality, read up and to the left from the F 4:3, is G 17:12, G 3:2, G 19:12, A 5:3, A 7:4, B 11:6, B 23:12, C 1:1. Start the scale at that C as root, and pick the best 12 notes from all in the F otonality 16 to create a mode that is relatively close to Just major scale.
The next columns in the chart are the closest 24-EDO root of the scale, the actual root as a ratio, and the name of the o/u tonality 16 note scale that was used to derive a new scale. The next column, labelled “Mode” is which of the 22 modes are applied to determine the 12 note scale in use.
For Follia, I only needed C, d, A, F, and g. Easy peasy. C, and F were straight otonal scales. D minor was a straight utonal scale. G minor was the 7:6 subminor based on the C otonality starting 3:2 above the root. A major was derived from the F otonal scale, starting at the A a 5:4 above the fundamental and going up from there.
Allemande was much more complex. For this piece, I needed nine keys, and almost none were straight otonal or utonal. I tried many different modes and scales before settling on a set. The challenge of finding reasonable sounding keys was very time consuming, so I resorted to sorting the potential scales based on how close it was to an ideal Just major or minor scale.
