The traditional 12 tone scale can be described in python code as np.array([‘C♮’, ‘D♭’, ‘D♮’, ‘E♭’, ‘E♮’, ‘F♮’, ‘G♭’, ‘G♮’, ‘A♭’, ‘A♮’, ‘B♭’, ‘B♮’]), or the enharmonic equivalent as np.array([‘C♮’, ‘C♮’, ‘D♮’, ‘D♮’, ‘E♮’, ‘F♮’, ‘F♮’, ‘G♮’, ‘G♮’, ‘A♮’, ‘A♮’, ‘B♮’]). Those are basically the notes that Bach used to notate his music (with the exception of B♮ which was called “H” and “B♭” was called “B”). Go figure.
I’m working on a way to improve the sound of some synthetic chorales generated by the Deep Neural Network model known as TonicNet. I’m most interested in the synthetic chorales that have a high degree of pitch entropy. I use the python library known as muspy to evaluate the generated chorales looking for those that have a high pitch class entropy.
The pitch class entropy is defined as the Shannon entropy of the normalized note pitch class histogram.
The formula according the the muspy documentation is:
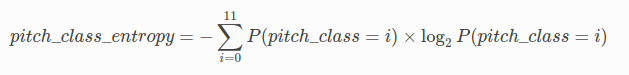
It basically gives a higher score if the pitches used include a lot of notes not in the root scale of the piece. A score over 3 contains a lot of notes outside the root key.
I used the TonicNet neural network to synthesize around 5000 unique chorales in S-A-T-B format, four voices, any number of notes each. I selected the highest scoring chorales, in terms of Pitch Class Entropy, and studied them for some ideas.
I tried retuning them using some standard Well Temperaments, and obtained some nice results. But I thought I might be able to improve on them if I used an adaptive tuning. William A. Sethares has a paper on the subject here: adaptive tuning.
I still need to code it up. But I thought it would be useful to describe what I am trying to accomplish first.