Author: Prent Rodgers

I’ve revised the arpeggios and fixed a few wrong notes in my version of the Chaconne by J.S. Bach as transcribed for piano left hand by Brahms. I previously didn’t make the arpeggios flow from bottom to top, but they do now. It sounds more pianistic this way. The tuning is still based on three scales:

1. D minor based on the Utonality on D
2. A major based on the Otonality on F, starting a 5:4 above the F
3. D major based on the same Utonality on D, but picking different notes

More info on this work can be found here, here, here, and here.

or download here:
Chaconne #8

I completed the 9th through 24th measures of Sarabande and this version is more or less complete. I may run a few more iterations of the randomizer and see how that changes things. I divided each measure into three, a quarter note per choice. For each quarter not, the preprocessor picks either a straight version, or one with arpeggios of different speeds and directions (up, down, or random), with quick moving pairs of notes turned into a glissando, and whacked out arpeggios far into the upper ranges of an otonality or utonality. For this version, I’ve made it possible to change to a different base otonality or utonality in the middle of a measure, instead of forcing it to stay for a whole measure in one scale. For example, measure 23, the second to the last, foes from F major otonality, to Bb major otonality, to F, then C major otonality. This forces some different Bb’s, some as the 7th overtone of C, some as a 16/9. It just sounds Just to me.
See more information on this piece here, & here.
I made the trills have the same number of steps as those recommended by C.P.E. Bach “trillo”, but through bending instead of discrete notes. Because I can, I guess. Some will find this strange.

Here’s a picture of the pitch modifier used in Csound to match the Bach recommendation.

See measures 4 & 5 for their use.

or download here:
Sarabande #5

Note: There was a bug in my Csound code that affected measure 11. It was an occasional reference to an invalid table. I reran the preprocessor, and it escaped this time without the error.
For geeks, here’s the source code to the preprocessor,
Here’s the Csound score it produced.

This version is similar to yesterdays, except for the keys used and some additional variations on the held chords on the second beat of the measures.

I moved the F major and C major keys to become based on their respective Otonality. I did not use the 11:8 as the 4th degree of the scale, but rather the 21:16, which is closer to a normal 4:3. Likewise the 6th degree of the scale is not the 13:8, but rather the 27:16, which is closer to a 5:3, a sweet sounding just ratio for the 6th degree of a scale. In sum, for a major scale, the ratios for the keys of C & F are:

• 1 C 1:1
• 2 D 9:8
• 3 E- 5:4
• 4 F 21:16
• 5 G 3:2
• 6 A 27:16
• 7 Bb 7:4
• 8 B 15:8
• 1 C 2:1

or download here:
Sarabande #2

Today’s work is a realization of the first eight measures of Bach’s English Suite #3 (BWV 809) Sarabande movement. The sarabande dance was first mentioned as a dance performed by Spanish colonists in the new world in the 16th century, thought indecent by some. Jesuit priests claimed it incited bad emotions in even very decent people.

By the time that Bach composed his English Suites, perhaps around 1718, it was considered a slow traditional dance form. What interested me about the piece is the interpretation of ornamentation. In the version that Glenn Gould recorded in 1977, he goes really wild with improvisational transformations of the written score. He has trills, rubato, glissando, and other ornaments that are not to be found in the score I have. Since I like to transform things, I decided to try my hand at it.

For this version, I created five or six variations for each quarter note beat in the 3/4 time signature. The software selects which 1/4 note duration to play at any given time. Some alternatives include glissandi (real ones), others have rubato, stretching notes across beats, and other changes.

The tuning is taken from several otonal and one utonal 16 note vectors in the 31-limit tonality diamond.

The keys of F, Bb, and D major are derived from the otonality of A#. The C and A major are derived from the otonality on F. G major is derived from the otonality on C, and the D minor is from the D utonality.

or download here:
Sarabande #1

I’ve revised some of the dynamics to decrease the accent on the first beats of the measures, and fixed some typos. More info on this work can be found here, here, and here.

or download here:
Chaconne #6

I’m nearing completion on the Brahms transcription for piano left hand of Bach’s Violin Partita No.2 in D minor, BWV 1004, the Chaconne movement. Today’s version has all the measures, but a few wrong notes and octaves that I still need to take care of.

The piece is basically an ostinato in D minor and A major, with many passing chords in other keys, and a section where he shifts to D major, then back to D minor.

I chose one otonality for A major, and a utonality for D minor. In my 31-limit tonality diamond, each o/utonality has 16 notes. Here are the notes in each relative to a 1:1 on C:

D minor

• 1 D 9:8
• 2 E- 27:22
• 3 F 27:20
• 4 G 3:2
• 5 A 27:16
• 6 A# 27:14
• 7 B 27:25
• 8 D- 27:25
• 9 E+ 9:7
• 10 F# 27:19
• 11 G# 27:17
• 12 A+ 54:31
• 13 B 54:29
• 14 C 1:1
• 15 C+ 27:26
• 16 D# 27:23

A major

• 1 A 5:3
• 2 B 23:12
• 3 C+ 25:24
• 4 D 9:8
• 5 E 5:4
• 6 F# 19:12
• 7 G 3:2
• 8 G# 19:12
• 9 A+ 7:4
• 10 B- 11:6
• 11 C 1:1
• 12 D- 13:12
• 13 D+ 7:6
• 14 E- 29:24
• 15 E+ 31:24
• 16 F 4:3

In the following chart, I show the entire 31-limit diamond, with the D minor utonality and scale in pink, and the A major on the F utonality. Note that the A major starts it’s 5:3 6 notes up to otonality. And the D minor starts 9 notes down the utonality. I’m still working through the tuning. Click on the graphic for an enlarged version.

or download here:
Chaconne #3

This is a new piece I’m just starting to work on. It’s based on Bach’s Violin Partita No.2 in D minor, BWV 1004, transcribed by Brahms for piano left hand. This piece has been performed and written about for centuries. Here’s a short essay, “About the Piece” as prepared for the LA Philharmonic by Grant Hiroshima.

Bach’s Chaconne for solo violin is a summit of Western music: as a technical and musical challenge, the violinist’s Everest. But musicians have not been content to leave this masterpiece solely in the fiddle’s intimate four-stringed domain. The famed conductor Leopold Stokowski created an immense orchestral version in the 1930s. And pianists have long made the Chaconne a concert favorite in the elaborate and virtuosic transcription by the legendary Italian pianist Ferruccio Busoni.

But they say tennis is no fun without a net. And in crafting his austere and perhaps more reverential vision, Johannes Brahms was seeking a different musical truth. Presenting his transcription to Clara Schumann (his friend and the widow of Robert Schumann), Brahms wrote: “The Chaconne is, in my opinion, one of the most wonderful and most incomprehensible pieces of music. Using the technique adapted to a small instrument, the man writes a whole world of the deepest thoughts and most powerful feelings. If I could picture myself writing, or even conceiving, such a piece, I am certain that the extreme excitement and emotional tension would have driven me mad. If one has no supremely great violinist at hand, the most exquisite of joys is probably simply to let the Chaconne ring in one’s mind. But the piece certainly inspires one to occupy oneself with it somehow…. There is only one way in which I can secure undiluted joy from the piece, though on a small and only approximate scale, and that is when I play it with the left hand alone…. The same difficulty, the nature of the technique, the rendering of the arpeggios, everything conspires to make me feel like a violinist!”

Majesty and vastness are easily conjured when two hands and a grand piano, or for that matter a full symphony orchestra, are called into service. But it is far more challenging to recognize that the true genius of the Chaconne is that it achieves its immenseness within the confinements of a single violin, and then to seek to inhabit on the piano this achievement with just the left hand alone.

Never shy to follow in the footsteps of giants, I’m venturing off to see what I can do to the piece with my 31-limit tonality diamond and my microtonal slide Bosendorfers.

I’ve only completed the first 16 measures, as written by Brahams below. The basic idea is to take the notes, durations, and velocities, and mix them up using the drunkard walk. The keys are well represented by the the Otonality and Utonality, with some modes taking the scale from different origins. The Chaconne is a four measure ostinato in the bass, more or less. And it soon gets very complex.

or download here:
Chaconne #3

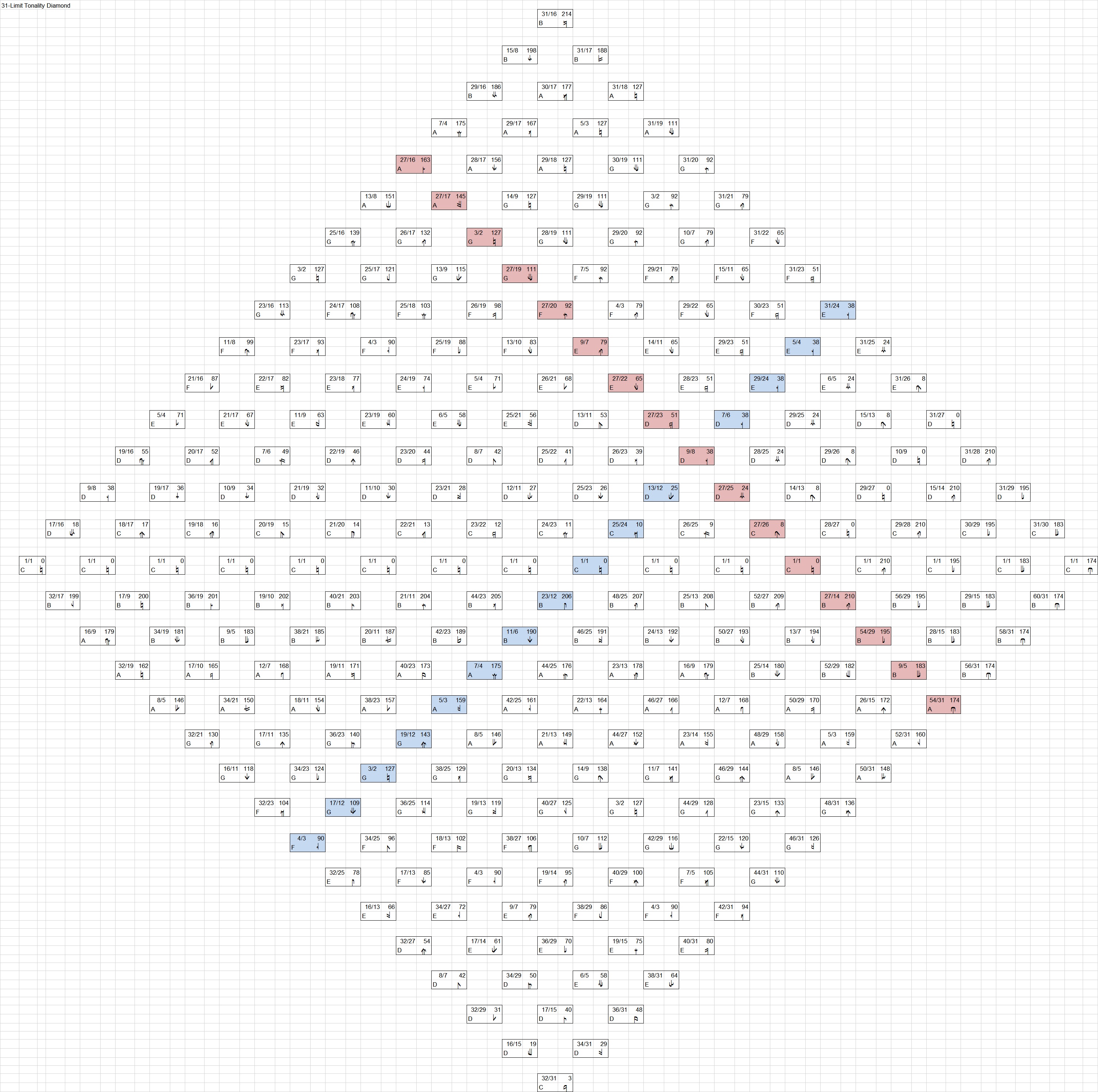
I have sets of 16 note scales derived from the 31-limit tonality diamond. The Otonality is the overtones, the Utonality are the undertones. Otonal scales have the ratios of 8:9:10:11:12:13:14:15:17:19:21:23:25:27:29:31. The Utonal scales are the opposite: 32 over 16:17:18:19:20:21:22:23:24:25:26:27:28:29:31.
That gets me a matrix that is 16 by 16, or 256 notes. Click the following image to enlarge it.

Elimintating duplicates, there are 216 unique pitches per octave. Right out of the gate I have 16 major 16-note scales based on the otonality, and 16 minor scales based on the utonality. Otonality is read up and to the right, Utonality is read down and to the right, except the scale starts at the note a 3:2 below the starting point. For example, Utonality of F is on the row starting at C 1:1, and the root of the scale is F 4:3.

When I was working with the 15-limit diamond, I noticed that there were other scales, in addition to major and minor, that could be found in the diamond. In 15-limit diamond, there are two additional scales with very good 5th’s. I called one the sub-minor with a 7:6 3rd, and the other a super-major with a 9:7 3rd.

When I took a systematic look at the otonality and utonality scales in the 31-limit diamond I found other modes that could be used to construct scales with perfect major 5ths. By other modes, I mean out of each 16 note scale, start at different points in each to find interesting scales. Limiting the search to only those with perfect 5ths, I found 22 distinct modes, and with the 16 otonal and 16 utonal scales, that left a total of 191 unique and interesting scales.

The 3rds are anywhere from 7:5 subminor to 31:24 sensi supermajor.

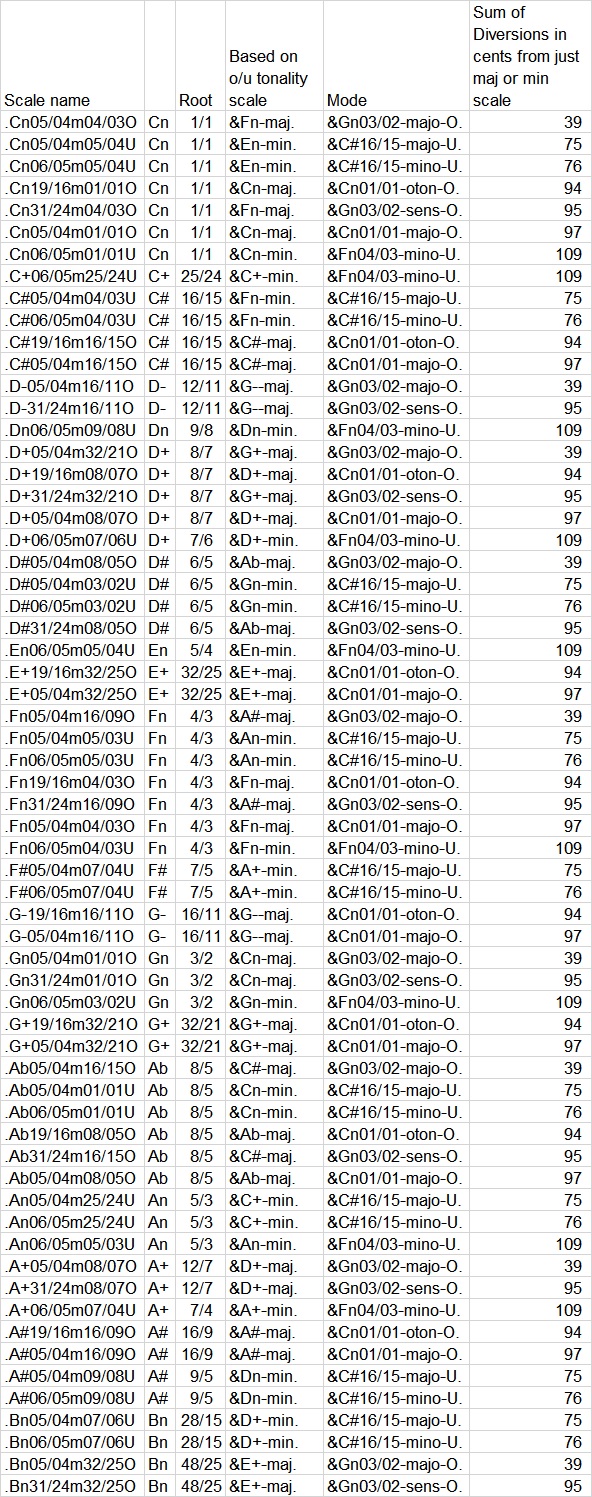
I then checked the other notes out for closeness to major or minor just. I evaluated the 2nds, 4th’s, 6th’s, and two different 7ths to see how many cents off each was, and then sorted them by distance from just. I ended up with 40 that were pretty good. In the chart below, the first column is the scale name. The first letter of the scale name is the root, the second two numbers are the third ratio, and the last two numbers are the root of the otonal (O) or utonal (U) from which the scale was derived.

For example, the first in the list starts on C, and has a 5:4 major third, and is derived from the otonal scale in the key of F. In the tonality diamond, the F otonality starts in the 9th position along the axis starting at C 1:1, then B 32:17, then A 16:9, then A 32:19, A 8:5, G 21:21, G 16:11, F 32:23, F 4:3. So the F 4:3 otonality, read up and to the left from the F 4:3, is G 17:12, G 3:2, G 19:12, A 5:3, A 7:4, B 11:6, B 23:12, C 1:1. Start the scale at that C as root, and pick the best 12 notes from all in the F otonality 16 to create a mode that is relatively close to Just major scale.

The next columns in the chart are the closest 24-EDO root of the scale, the actual root as a ratio, and the name of the o/u tonality 16 note scale that was used to derive a new scale. The next column, labelled “Mode” is which of the 22 modes are applied to determine the 12 note scale in use.

For Follia, I only needed C, d, A, F, and g. Easy peasy. C, and F were straight otonal scales. D minor was a straight utonal scale. G minor was the 7:6 subminor based on the C otonality starting 3:2 above the root. A major was derived from the F otonal scale, starting at the A a 5:4 above the fundamental and going up from there.

Allemande was much more complex. For this piece, I needed nine keys, and almost none were straight otonal or utonal. I tried many different modes and scales before settling on a set. The challenge of finding reasonable sounding keys was very time consuming, so I resorted to sorting the potential scales based on how close it was to an ideal Just major or minor scale.

Another run through the algorithm produced these variations on Arcangelo Corelli’s Folia Opus 5, a piece written just prior to 1700, for violin and continuo. Folia is a chord progression well used in the 15th and 16th centuries by a variety of composers. Think of it as the 12-bar blues of early classical music tradition. Corelli’s version is a theme with 23 variations. My version intersperses the theme with the variations, as I did with the Allemande.

This version is scored for my microtonal slide Bosendorfers, realized in Csound. The tuning uses two otonalities (based on C & F), one utonality (D), plus a few mixed tunings (an A major based on the F otonality, and G minor based on the C otonality) from the 31-limit diamond.

or download here:
Follia #4

I present here some variations on Arcangelo Corelli’s Folia Opus 5, a piece written just prior to 1700, for violin and continuo. Folia is a chord progression well used in the 15th and 16th centuries by a variety of composers. Think of it as the 12-bar blues of early classical music tradition. Corelli’s version is a theme with 23 variations. My version intersperses the theme with the variations, as I did with the Allemande.

This version is scored for my microtonal slide Bosendorfers, realized in Csound. The tuning uses two otonalities (based on C & F), one utonality (D), plus a few mixed tunings (an A major based on the F otonality, and G minor based on the C otonality) from the 31-limit diamond.

or download here:
Follia #6